Fractal Renderer
Project Overview
In my first semester of grad school, as part of the Generative Methods in Computer Graphics course, I collaborated with my group to create a program that renders a Mandelbulb using signed distance functions (SDFs) in OpenGL. This course focused on procedurally generating graphics programs, and for our final project, we chose to explore the complex world of fractals.
Our project began with a path tracing algorithm to render a voxel representation of a Mandelbulb. However, this approach resulted in massive data sizes and slow, low-resolution rendering. To address these challenges, we transitioned to using ray marching to render an SDF, which enabled us to achieve much higher detail and real-time performance.
What is a Mandelbulb?
A Mandelbulb is a three-dimensional fractal, an extension of the two-dimensional Mandelbrot set. Unlike the flat Mandelbrot set, the Mandelbulb extends into 3D space, creating intricate, self-similar patterns. Fractals like the Mandelbulb are fascinating because they exhibit infinite complexity, with each zoom revealing new structures.
Implementation Details
Initial Approach: Voxel Representation
- Utilized a path tracing algorithm to render a voxelized Mandelbulb.
- Caching the voxel data was necessary, but it resulted in enormous data size and sluggish performance.
- Due to the need to cache the voxel data, the Mandelbulb was a static object.
- The voxel version, while functional, was limited to low-resolution outputs.
- Final Approach: SDF with Ray Marching
- Transitioned to ray marching for rendering a signed distance function.
- This approach dramatically increased detail and allowed for real-time rendering.
- The ray marching technique involves tracing rays through the scene and using distance functions to determine the intersection with the fractal surface.
- Because the SDF returns a surface, we were able to implement a simple Blinn-Phong lighting model.
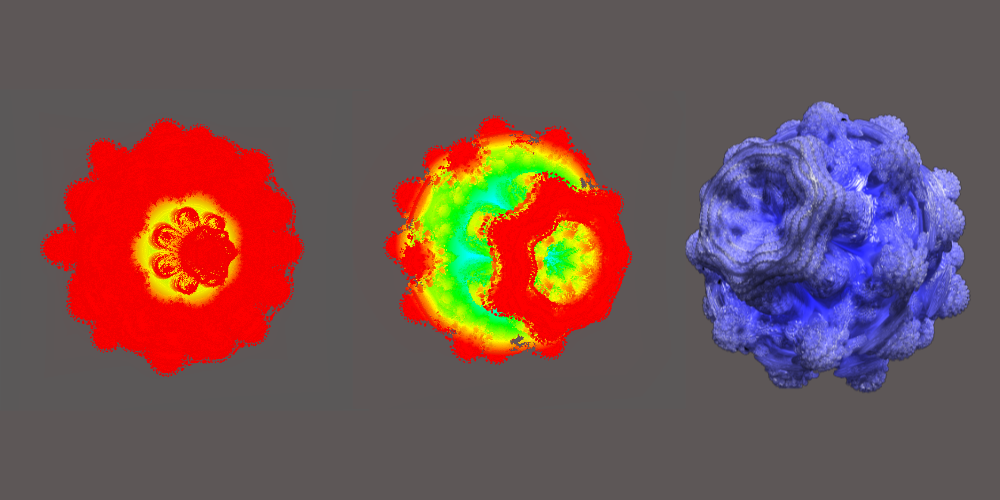
Below are examples of the voxel approach. On the left is a voxel grid with side lengths of 1,000 voxels, and on the left is a grid with dimensions of 512 voxels. The color differences between the two voxel Mandelbulbs is due to how coloring was calculated based on density. The final Mandelbulb on the right is the final result of the SDF combined with Ray Marching.
To achieve real-time rendering of the Mandelbulb, we used a ray marching algorithm combined with a signed distance function (SDF). Below is a snippet of glsl code showcasing the distance function used to calculate the surface of the Mandelbulb.
// Mandelbulb Signed Distance Function
float x = pos.x;
float y = pos.y;
float z = pos.z;
float delta_rad = 1.0;
float rad = 0.0;
for (int i = 0; i < NUM_ITERATIONS; i++) {
rad = length(vec3(x, y, z));
if (rad > 2.0) {
iterations = i;
break;
}
// convert to polar coordinates
float theta = acos(z / rad);
float phi = atan(y, x);
delta_rad = pow(rad, order - 1.0) * order * delta_rad + 1.0;
// scale and rotate the point
// changing the value of the order variable morphs the Mandelbulb
float zeta_r = pow(rad, order);
theta = theta * order;
phi = phi * order;
// convert back to cartesian coordinates
x = zeta_r * sin(theta) * cos(phi) + pos.x;
y = zeta_r * sin(phi) * sin(theta) + pos.y;
z = zeta_r * cos(theta) + pos.z;
}
return 0.5 * log(rad) * rad / delta_rad;
Features
- Real-Time Rendering: The SDF approach enables smooth, high-resolution rendering of the Mandelbulb in real time.
- Interactive Exploration: Users can explore the fractal by rotating and zooming, revealing its intricate structures.
- Dynamic Morphing: The Mandelbulb can morph, demonstrating changes in its order and structure.
- Soft Shadows: A feature of the ray marching algorithm allows for dynamic lighting calculated in real time, as demonstrated below:
// Soft Shadow Function
float shadow_strength = 1.0;
float current_distance = 0.0;
float step_size = float(MAX_DISTANCE) / float(MAX_STEPS);
for (int i = 0; i < MAX_STEPS; i++) {
vec3 current_position = ray_origin + light_direction * current_distance;
float distance_to_surface = DistanceEstimate(current_position);
if (distance_to_surface < EPSILON) {
return 0.0; // The point is in shadow
}
// decay_factor determines the softness of the shadow
float shadow_attenuation = decay_factor * distance_to_surface / current_distance;
shadow_strength = min(shadow_strength, shadow_attenuation);
current_distance += step_size;
if (current_distance >= MAX_DISTANCE) {
break;
}
}
return shadow_strength;
Videos and Screenshots
Project Overview Video (4 minutes): A comprehensive walkthrough of the program’s features and capabilities.
- Mandelbulb Rotation Video: A captivating visualization of the Mandelbulb rotating and morphing.
Reflections and Learnings
Through this project, I gained valuable experience in advanced rendering techniques, particularly the power and flexibility of SDFs and ray marching. The transition from voxel to SDF rendering taught me the importance of optimizing data representation for performance. This project has also deepened my appreciation for the beauty and complexity of fractal geometry.
Additional Resources
- Presentation Slides: Download
- Code Repository: GitHub Link